この記事はVoicy Advent Calendar 2022の14日目の記事です。
TL;DR
- pythonのnetworkxを触ってみたい
- 社内制度の「ボ祝儀」のデータを対象にして社員同士の感謝でネットワークを作成
- 作成したネットワークの基礎的な指標からネットワークの特性の把握, 頂点の中心性から中心人物の特定
- 今後の展望としてクラスタリング、中心性の時系列推移などが考えられる
参考になりそうな人
はじめに
こんにちは!株式会社Voicy データチームのイシケンです。 今回は「Voicyのメンバー同士の感謝をネットワークにして遊んでみたよ」というお話です。
モチベーションとしては、学生時代にR言語のigraphを用いてネットワークを扱ったことがあるのですが、pythonでネットワークを扱った経験がないので基本的な操作を通して感覚を掴みたいという点になります。
感謝とはなんぞ?
今回ネットワークを構築する際のデータの対象とした「感謝」について説明します。
Voicyでは「ボ祝儀」と呼ばれる社員同士で報酬を送り合うピアボーナス制度を導入しています。具体的にはSlack上で、感謝を送りたい人に感謝のメッセージとポイントを送り、もらったポイントはTシャツなどのVoicy社員限定のアイテムに交換することができるという制度です。
ボ祝儀の例をあげると、「難易度の高い仕事を自ら引き受けてくれた。」「お願いしていた以上のスピードで依頼した仕事を行ってくれた。」などなど、リスペクのを感じる行動に対してその気持ちを言葉にして伝えるような内容がボ祝儀として送られています。
このボ祝儀のデータから「誰が誰に感謝を送ったか」のネットワークを構築してみました。
また、ボ祝儀データの期間は2022/8/1 ~ 2022/10/31の3ヶ月間としました。弊社は下期が8月~1月末であり、直近のクォーターが3Qの2022/8/1 ~ 2022/10/31であるためこの期間としました。
データの形は以下の画像のようなエッジリスト形式のcsvデータを準備しました。senderがボ祝儀送信者, receiverがボ祝儀受信者を表しています。
ボ祝儀(感謝)ネットワークの構築
今回はpythonのnetworkxを用いてネットワークの構築・描画などを行いました。グラフは有向グラフとして作成し、プロットしてみます。コードとプロットした画像は次のようになります。
import pandas as pd import networkx as nx import matplotlib.pyplot as plt # 用意したデータの読み込み edge_list = pd.read_csv('edge_list.csv') # エッジリストから有向グラフを作成 G = nx.from_pandas_edgelist(edge_list, source='sender', target='receiver', create_using=nx.DiGraph()) # 描画領域の準備 plt.figure(figsize=(10,10)) # 描画用のレイアウトの計算 pos = nx.spring_layout(G, weight=None, k=1) # 描画用の頂点の設定 nx.draw_networkx_nodes(G, pos, node_size=100, alpha=0.7, linewidths=0, node_color='#FF7D32') # 描画用の辺の設定 nx.draw_networkx_edges(G, pos, width=1.5, edge_color='#AAAAAA', style='-', alpha=0.7, arrowstyle='->', arrows=True) # 描画する plt.show()
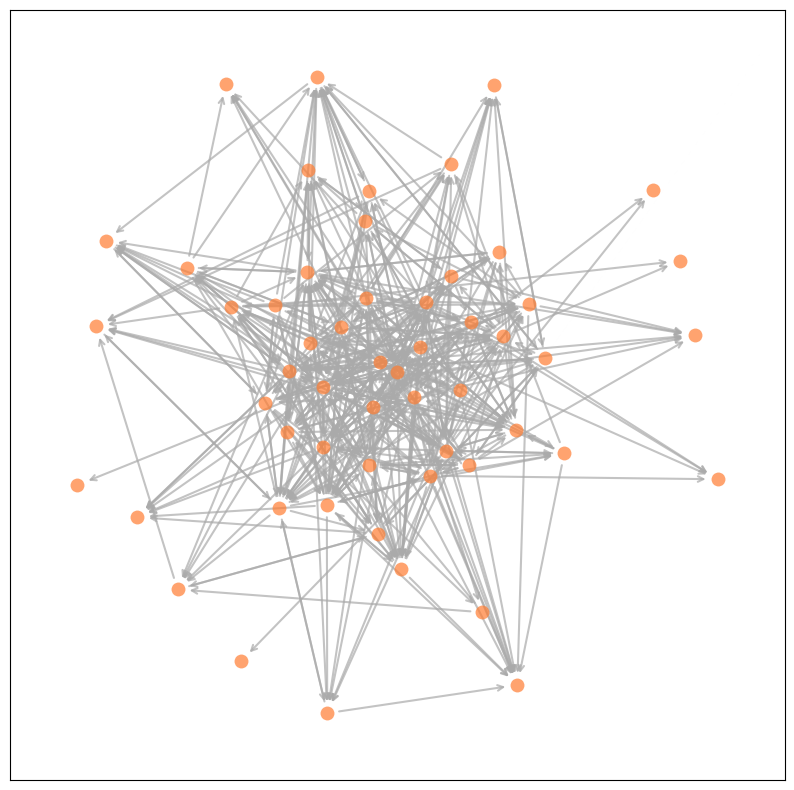
次はグラフ全体の基本的な情報を確認していきます。
print(nx.info(G)) print('L=', nx.average_shortest_path_length(G)) print('C=', nx.average_clustering(G))
DiGraph with 55 nodes and 486 edges L= 1.7316498316498317 C= 0.2630020063879922
nx.info(G)により社員を表す頂点が55こ、ボ祝儀の送信を表す辺が486こであることがわかります。
nx.average_shortest_path_length(G)で、このネットワークの平均距離を求めることができます。ネットワークの平均距離とは全ての2頂点の組み合わせの最短距離の平均になります。このネットワークの平均距離は1.7でした。誰かと繋がりたいようなときは間に一人立たせることでおおよその人とは繋がることができるということが読み取れます。
nx.average_clustering(G)で、このネットワークのクラスタ係数を求めることができます。クラスタ係数は各頂点についての値で、ある頂点から繋がっている2つの頂点も繋がっている割合になります。この値の平均を取ることでネットワークのクラスタ係数の計算が可能です。現実に存在するネットワークのクラスター係数は0.1から0.7程度といわれているので、一般的な社会ネットワークの範疇ではあるが低い値であると言えそうです。
次数
次は頂点の次数を確認していきます。ネットワークにおける頂点の次数とは頂点から伸びている辺の本数のことを表します。 今回作成したネットワークは辺に向きが存在している有向グラフですので、頂点から出ていく辺(=ボ祝儀を送信した)と頂点に入ってくる辺(=ボ祝儀を受け取った)の2種類が存在します。
算出する際は辺の重みは考慮しない形で計算を行っています。つまりAさん → Bさんで2回ボ祝儀を送信していた場合とAさん → Bさんで1回ボ祝儀を送信していた場合の価値は同じになります。「ボ祝儀を送受信した回数」ではなく、「ボ祝儀によりどれだけ多くの人と関係性を構築しているか」で評価をするイメージになります。
それぞれの次数について、top5を表示した際のコードは以下のようになります。
# 頂点から出ていく辺の次数のtop 5をソートして表示 print(sorted(G.out_degree(weight=None), key=lambda x: x[1], reverse=True)[0:5]) # 頂点に入ってくる辺の次数のtop 5をソートして表示 print(sorted(G.in_degree(weight=None), key=lambda x: x[1], reverse=True)[0:5])
頂点から出ていく辺の次数が最も高かった、つまり最もボ祝儀を多くの人に送信していたのは広報のかなみんさんでした。 かなみんさんが送信しているボ祝儀を確認したところ、「業務領域で関わる人たちに留まらずに感謝を伝えている。他の社員の行動に対するアンテナの感度が高い。」といった素敵な特徴が見えました。
頂点に入ってくる辺の次数が最も高かった、つまり最もボ祝儀を多くの人から受け取っていたのは人事労務ののんちゃんでした。 のんちゃんが受け取っているボ祝儀を確認したところ、「かなみんさん同様に業務領域で関わる人たちに留まらず多くの社員から感謝を受け取っている。コミュニケーション能力の高さと軽快なフットワークによる社員交流の多さ、高い当事者意識による質の良いアウトプットが評価されている。」などの素敵な特徴が見えました。
僕自身、かなみんさんからボ祝儀を受け取ったことがあり、のんちゃんへボ祝儀を送ったことがあるため非常に納得度の高い結果となりました。
中心性
上記の次数の結果は元のデータをカウントしていけば出力できるデータでした。次はネットワークならではの指標である中心性を算出してみようと思います。
今回は媒介中心性, 近接中心性, 固有ベクトル中心性でネットワークの中心人物を定量的に探してみたいと思います。
媒介中心性は、ある頂点がそれ以外の2つの頂点間の最短経路にどのくらいの割合で入っているかを表す値です。「誰かを人伝いに紹介してもらうときに、とりあえずこの人に相談しよう」というイメージです。
近接中心性は、ある頂点が他の頂点まで平均的にどれくらい近いかを表す値です。「直接の関係性がない人も含めた他の人との平均距離」のイメージです。
固有ベクトル中心性は、中心的な頂点と繋がっている頂点は中心的であるという考え方の指標です。「中心人物と関係がある人も中心的な人」のイメージです。
それぞれの中心性は以下のコードで算出することができます。
# 媒介中心性 bet_cent = nx.betweenness_centrality(G) # top3の頂点を表示 list(sorted(bet_cent.items(), key=lambda x:x[1], reverse=True)[0:3]) # 近接中心性 clo_cent = nx.closeness_centrality(G) print(sorted(clo_cent.items(), key=lambda x:x[1], reverse=True)[0:3]) # 固有ベクトル中心性 eig_cent = nx.eigenvector_centrality(G) print(sorted(eig_cent.items(), key=lambda x:x[1], reverse=True)[0:3])
算出した結果、全ての中心性において人事労務 のんちゃんがトップであることが明らかとなりました! 今回は有向グラフで構築したため、ボ祝儀を最も受け取っていたのんちゃんが中心人物であることに違和感はないと思います。
結論
社員に感謝を伝えるときは、ボ祝儀を最も多くの社員に送っていたかなみんさんを参考にする。
社員から感謝をもらえるようなバリューを出すためには、ボ祝儀を最も受け取っていたのんちゃんを参考にする。
話したことがない社員を紹介してもらうときには、一種の人間関係を表すネットワークの中心人物であるのんちゃんにお願いするのが効率的である。また、ネットワークの平均距離が1.7であったことから、のんちゃんから直接繋がりたい相手と繋がることができると考えられる。
おわりに
今回は「ボ祝儀」という弊社特有の行動をもとに社員同士の感謝のネットワークを構築しました。 また、構築したネットワークに対して幾つかの指標を確認することで、ネットワークの特性の考察、中心人物の捜索を行いました。
今後の展望としては
- 構築したネットワークをクラスタリングした際にどのようなクラスターに分かれるかの検討
- 中心性を時系列で算出することで、中心的人物は中心性が成長して中心になったのか、あるいは登場した時から中心的なのかを検討する
などが考えられます。
明日は、QAエンジニアの@kodai-matsumotoさんです!